The principles of artistic illusions (ISOMETRIC DRAWINGS)

Illusory works of art have a curious fascination. They represent a triumph of art over reality. They are illogic masquerading as logic.

Why do illusions capture our interest? Why have so many artists gone to the trouble to produce them? Mountain climbers say they scale mountains "because they are there." Perhaps we seek illusions because they aren't there.

We have all admired the lithograph Waterfall by Maurits C. Escher (1961). His waterfall recycles its water after driving the water wheel. If it could work, this would be the ultimate perpetual motion machine that also delivers power! If we look closely, we see that Mr. Escher has deceived us, and any attempt to build this structure using solid masonry bricks would fail.

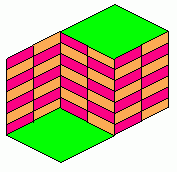
ISOMETRIC DRAWINGS

Two-dimensional drawings (on a flat surface) can be made to convey an illusion of three dimensional reality. Usually this deception is employed to depict real, solid objects in spatial relationships achievable in our world of sensory experience.

The conventions of classical perspective are very effective at simulating such reality, permitting `photographic' representation of nature. This representation is incomplete in several ways. It does not allow us to see the scene from different vantage points, to walk into it, or two view objects from all sides. It does not even give us the stereoscopic depth sensation that a real object would have due to the lateral separation of our two eyes. A flat painting or drawing represents a scene from only one fixed viewpoint, as does an ordinary monocular photograph.

One class of illusions appears at first look to be ordinary `perspective' renderings of solid, three dimensional objects or scenes. But on closer examination, they reveal internal contradictions such that the three dimensional scene they depict could not exist in reality. These pictures have a special fascination for those of us used to the convention of depicting nature on a flat surface of paper, canvas, or in a photograph.

Isometric illusory art was created as early as 1934 by Swedish Artist Oscar Reutersvärd with the impossible arrangement of blocks shown here. The colors in this version are not to be blamed on Oscar. This design has been widely used, and even appears on a Swedish postage stamp.

THE PENROSE ILLUSION

One particular example of the Reutersvard illusion is sometimes called the `Penrose' or `tribar' illusion. Its simplest form is illustrated here.

The picture appears to depict three bars of square cross section joined to form a triangle. If you cover up any one corner of this figure, the three bars appear to be fastened together properly at right angles to each other at the other two corners–a perfectly normal situation. But now if you slowly uncover a corner it becomes apparent that deception is involved. These two bars that connect at this corner wouldn't even be near each other if they were joined properly at the other two corners.

The Penrose illusion depends on `false perspective,' the same kind used in engineering `isometric' drawings. This sort of illusion picture displays an inherent ambiguity of depth, which we will call `isometric depth ambiguity.'

Isometric drawings represent all parallel lines as parallel on the flat page, even if they are tilted with respect to the observer in the actual scene. An object tilted away from the observer by some angle looks the same as if were tilted toward the observer by the same angle. A tilted rectangle has a two-fold ambiguity, as demonstrated by Mach's figure (right), which may be seen as an open book with pages facing you, or as the covers of a book, with the spine facing you. It may also be seen as two symmetric parallelograms side by side and lying in a plane, but few people describe it that way.

The Thiery figure (above) illustrates the same artistic deception.

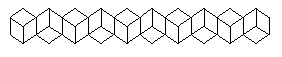
Schroeder's reversible staircase illusion is a very `pure' example of isometric depth ambiguity. It may be perceived as a stairway that one could ascend from right to left, or as the underside of a stairway, seen from below. Any attempt to draw this with vanishing points would destroy the illusion.

The simple design below looks like three faces of a string of cubes, seen either from the outside, or the inside. If you put your mind to it, you can see them as alternating: inside, outside, inside. But it's very hard, even if you try, to see at as simply a pattern of parallelograms in a plane. This is the same as the `tumbling blocks' design sometimes used in quilts.

Blackening some facets enhances the illusion, as is shown below. The black parallelograms at the top are seen either as from below, or from above. Try as hard as you can to see them as alternating, one from below, one from above, and so on, left to right. Most people can't. Why should we be unable to do this?

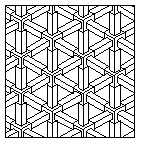
The design at the right uses the tribar illusion relentlessly in strict isometric drawing style. This is one of the `hatching' patterns of the AutoCAD (TM) computer graphics program. It is called the `Escher' hatching pattern.

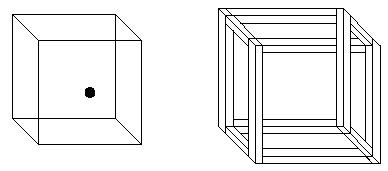
The isometric wire-frame drawing of a cube (below left) shows isometric ambiguity. This is sometimes called the Necker cube. If the black dot is on the center of a face of the cube, is that face the front, or the rear face? You can also imagine the dot is near the lower right corner of a face, but still you can't be sure if it is the front or rear face. You have no reason to assume that the dot is in or even on the cube, but might be behind or in front of the cube, since you have no clue to determine the relative size of the dot.

If the edges of the cube are given a suggestion of solidity, as if the cube were made of wooden 2x4s nailed together, a contradictory figure results. But here we have used ambiguous connectivity of the horizontal members, which will be discussed in the next section. This version is called the `crazy crate'. Perhaps it would serve as as the frame to build a shipping crate for illusions. Nailing the plywood faces onto the frame to complete the crate would be a real challenge, but necessary to keep the illusions from falling out!

 Back